How To Find Horizontal Displacement

A projectile is referred to equally any object launched into space with only gravity interim on it. Gravity is the primary strength that acts on a projectile. This doesn't imply that other forces do non act on a projectile; it'southward just that their touch on is minimal compared to gravity. The trajectory of a projectile is the path traveled by it. Some examples of a projectile in real life are a bullet fired from a gun, a javelin thrown by an athlete, or an arrow released from a bow.

Projectile Move

When an object is launched into the air, it travels along a curved path under constant acceleration that is directed toward the center of the Earth. The object that has been launched or thrown into the air is called a projectile. Some initial force must exist imparted upon an object to become a projectile, and the move of a projectile is referred to every bit projectile motion.

When an object is first launched into the air, it goes at a sure speed, known equally the initial speed or velocity. The angle of projection describes the angle with respect to the horizontal when the object is launched. The maximum height, range, and time of flight of a projectile are adamant by the initial speed and angle of projection of the projectile. The strength of gravity is the simply force acting on an object after it has been launched into the air, as the other forces have a negligible affect compared to gravity.

Trajectories of projectiles under diverse initial atmospheric condition

The maximum height and range of the projectile will change if at that place is an increase or decrease in the initial velocity or bending of projection. The height and range will increment with an increment in the initial velocity, while the affect of the alter in bending of project is unlike on the maximum height and range.

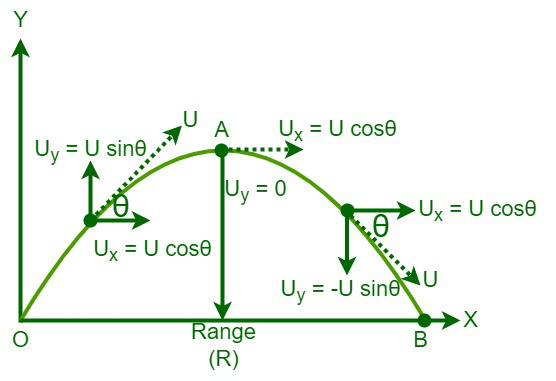
The effigy depicts the projectile motility of an object that was propelled at an angle of θ with an initial velocity of U. O is the point of projection. The object will ascend forth a parabolic path while being decelerated by gravity until it reaches its maximum height. The vertical component of the velocity diminishes as the object travels upward and becomes zero when it reaches the maximum height. Following that, the object will drop till it touches the ground while being pulled downward by gravity. The horizontal range, or range (OB), is the horizontal distance between the indicate of projection and the landing location. "Time of flight" is the total fourth dimension taken by the object from reaching O to B.

An important concept in projectile motion is that there are two simultaneous independent rectilinear motions:

Along the x-axis (or) Horizontal motility: The initial velocity and angle of projection are the sole factors that affect the horizontal motion of an object.
Along the y-axis (or) Vertical movement: The initial conditions (initial velocity and angle of projection) and the acceleration due to gravity are the factors that touch the vertical motion of an object.

Equations of Movement for a Projectile

Nosotros can brand apply of various equations of motility to find different parameters related to projectile motion.

If the initial velocity, acceleration, and time of flight are known, the last velocity can be adamant using the formula below.

5 = u + at

Where u is the initial velocity, a is the acceleration, and t is the time of flight.

Nosotros can also determine the deportation of a projectile using the initial velocity, dispatch, and time of flight, according to the formula beneath.

s = u t+ ½ at^two

If the time of flight is not given, and the displacement of the projectile is given, and then the final velocity can be calculated using the formula below.

v² = u^two + 2as

The initial velocity and bending of projection can exist used to calculate the horizontal component of the initial velocity.

U_x = U cos θ

The velocity in the horizontal direction will non modify as the projectile will non feel acceleration in this direction since the dispatch due to gravity acts vertically down. Hence,

5_x = U_x

Furthermore, the range or horizontal displacement of a projectile is dependent on the horizontal component of the initial velocity and time of flight. The equation for the range or horizontal displacement of a projectile is given equally,

x = U_x t

x = U cosθ t

Just similar the horizontal component, the vertical component of the initial velocity also depends only on the initial velocity and angle of projection. It can exist adamant using the formula below.

U_y =U sin θ

The velocity in the vertical direction will change as the projectile experiences dispatch due to gravity which acts vertically downward. Hence,

V_y = U sinθ − gt

Vertical displacement of a projectile

The maximum height, or vertical deportation, of a projectile, depends on the initial velocity, dispatch due to gravity, and time of flight. The equation for the vertical deportation or maximum height of a projectile is given as,

y = U_yt − ½ gt²

y = U sinθ t − ½ gt²

Where y is the vertical displacement of a projectile

U = initial velocity of the particle,

t = time of flight,

θ = angle of project, and

m = acceleration of gravity

Sample Questions

Question 1: Define projectile, projectile motility, and trajectory and write the equation of horizontal and vertical deportation in projectile motion.

Answer:

Projectile and projectile motility: When an object is launched into the air, information technology travels along a curved path under constant acceleration that is directed toward the centre of the Earth. The object that has been launched or thrown into the air is called a projectile and the motion of a projectile is referred to as projectile move.

Trajectory: The trajectory of a projectile is the path travelled by it.

Horizontal displacement in projectile motility: The horizontal range, or range, is the horizontal distance between the point of projection and the landing location. The range or horizontal displacement of a projectile is dependent on the horizontal component of the initial velocity and time of flight.

The equation for the range or horizontal displacement of a projectile is given as,

x = U cosθ t

Where x is the horizontal displacement of a projectile, U = initial velocity of the particle, t = time of flight, and θ is the angle of projection.

The vertical displacement in projectile movement: The maximum height, or vertical displacement, of a projectile, is the highest vertical position along its trajectory. It depends on the initial velocity, acceleration due to gravity, and time of flight. The equation for the vertical displacement or maximum pinnacle of a projectile is given equally,

y = U sinθ t − ½ gtⁱⁱ

Where y is the vertical deportation of a projectile, U = initial velocity of the particle, t = time of flying, θ is the angle of projection and g = acceleration of gravity

Question 2: A ball is launched at a velocity of 35 one thousand/southward in a direction, making an angle of lx° with the horizontal. Determine the vertical projectile displacement of the ball if the time interval is four seconds. (g = 9.8 m/s²)

Answer:

Given information,

Velocity (u) = 35 m/south

Time interval = four sec

Bending (θ) = 60°

Acceleration due to gravity = 9.8m/s2

We have,

Vertical deportation in the projectile motion of a particle is given by:

y = u sinθ t – ½ g t2

y = 35 × sin lx° × 4 – ½ × 9.eight × (four)2

= 121.243 – 78.4{sin 60° = √3/2}

= 42.84 m

Hence, the vertical projectile deportation of the particle is 42.84 m.

Question 3: Determine the vertical projectile displacement of a body launched at 50 1000/s in a direction that forms a 45° angle with the horizontal and the time interval is 2.5 sec. (yard = nine.8 m/s²)

Respond:

Given data,

Velocity (u) = 50 thousand/s

Time interval = ii.five sec

Angle (θ) = 45°

Acceleration due to gravity = 9.8m/southward²

We have,

Vertical displacement in the projectile motion of a particle is given by:

y = u sinθ t – ½ thou t²

y = 50 × sin 45° × two.five – ½ × 9.8 × (ii.5)2

= 88.388 – xxx.625 {sin 45° = ane/√ii}

= 57.763 m

Hence, the vertical projectile displacement of the particle is 57.763 g.

Question iv: Notice the velocity at which an object is launched, making an bending of 30° with the horizontal, and the vertical projectile displacement of the ball, and the fourth dimension interval are 35m and 5 seconds. (g = x yard/due south^two)

Reply:

Given data,

The vertical projectile displacement (y) = 35 m

Time interval = 5 sec

Angle (θ) = 30°

Dispatch due to gravity = 10 one thousand/due south²

We have,

Vertical displacement in the projectile motility of a particle is given by:

y = u sinθ t – ½ grand t²

⇒ 35 = u × sin 30° × 5 – ½ × x × (5)²

⇒ 35 = 2.v u – 125 {sin 30° = ½}

⇒ 2.5u = 160 ⇒ u = 64 m/s

Hence, the velocity at which an object is launched is 64 m/s.

Question five: A ball is launched at a velocity of xl m/s and the vertical projectile displacement of the ball and the time interval are 45m and 3.v seconds. Now, determine the angle that the ball forms with the horizontal. (g = 10 m/s2)

Answer:

Given data,

The vertical projectile displacement (y) = 45 m

Fourth dimension interval = three.5 sec

Velocity (u) = 40 m/southward

Acceleration due to gravity = 10 m/sⁱⁱ

We take,

Vertical displacement in the projectile move of a particle is given by:

y = u sinθ t – ½ g t²

⇒ 45 = twoscore × sin θ × 3.5 – ½ × 10 × (3.5)²

⇒ 45 = 140 sin θ – 61.25

⇒ 140 sin θ = 45 + 61.25 = 106.25

⇒ sin θ = 106.25/140 = 0.7589

⇒ θ = sin^-i(0.7589) = 49.37°